Fisica Teoria 2

Un operador hermítico puede descomponerse por sus autovalores y los proyectores a los autoespacios asociados a cada autovalor de la siguiente manera:

y hermitico.

El estado de todo sistema físico está representado por un vector (de norma
unidad) en un espacio de Hilbert ().

Dimensión = Cantidad de resultados de una medición exhaustiva

Todas las propiedades observables de un sistema físico se representan con
operadores lineales hermíticos que actúan sobre . Denominados

Un operador tiene autovalores y proyectores a sus autoespacios asociados

Los resultados posibles de la medición de cualquier observable son sus autovalores

Si el estado de un sistema es , la probabilidad de obtener el resultado en la medición del observable es siempre:

Si el estado de un sistema es y medimos el observable y detectamos el autovalor , entonces el estado del sistema después de la medición se obtiene a partir de la proyección de sobre el subespacio asociado al autovalor
El denominador es necesarrio para normalizar

El valor esperado (o medio) de se define para un estado implicito :
Que es igual a:
La dispersión de se define como:

Partiendo de la desigualdad de Shwarz que establece:
Y eligiendo los kets y

Se puede demostrar:

Aplicado a los operadores y

Un operador interactua con un estado puro mediante los postulados de probabilidad y colapso. Para el cálculo de la probabilidad:

El estado tambien se puede representar como el proyector con la propiedad

Si un estado puede estar en diferentes estados posibles cada uno con probabilidad se lo denomina un ensamble se puede hablar de un estado mixto descripto por el operador densidad (o matriz densdiad). La aleatoridad en este caso proviene de IGNORANCIA del sistema.
Este operador generaliza las propiedades de los estados puros. Los estados puros y sus probabilidades se lo puede pensar como la descomposición espectral del estado mixto.

Ademas:

Valor que cuantifica cuan puro o mixto es un estado

Bases ortonormales (Las bases canonicas son definidas para spin up y down en z):

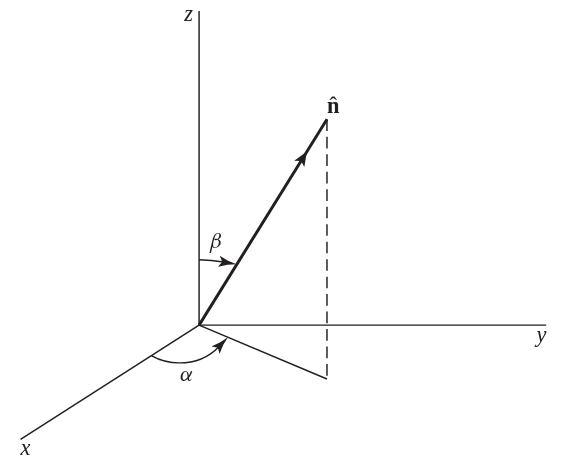
Spines en otras direcciones se definen:

Cumplen la propiedad que (Spin opuestos son ortogonales)
Cumplen la propiedad que (Spin opuestos son ortogonales)

Las mediciones que se pueden realizar consiste de medir el spin en una dirección y pueden ser +1 o -1. Si se respeta la base, los operadores son:
Donde , y son las Matrices de Pauli:

La medición de spin en la dirección corresponde al operador

El proyector al autoespacio asociado a la medición es

Si se mide spin en la dirección dada por los angulos y :

El operador asociado es:

Con los estados de spin +1 y -1 asociados:

Generalizando los estados de spin a matrices densidad:
𝟙Donde es el vector polarización.
El modulo de se relaciona con la pureza:
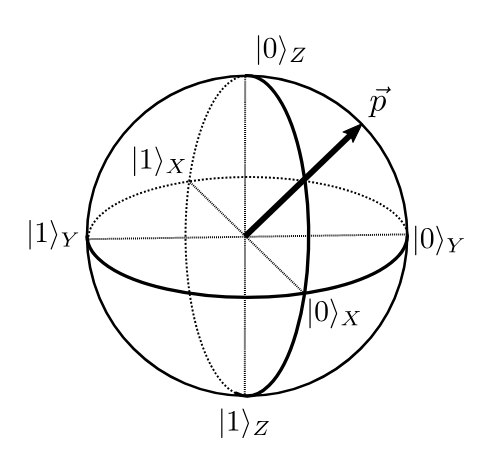
Se pueden representar en la esfera de Bloch:

Si uno tiene un sistema compuesto por dos subsistemas A y B con espacios de estados y el estado del sistema compuesto es un elemento del espacio

Este espacio tiene una base donde son los ket base de y son los ket base de .

Los estados de que son producto de dos estados de y se doneminan estados producto :

Si NO corresponde a el producto de dos estados, se donomina estado entrelazado.

La forma general de escribir un estado compuesto es:

Dada la base de operadores sobre y denodadas y , con dimensiones y respectivamente se definen los operadores sobre :

La traza parcial de un operador sobre y se definen:

La matriz densidad reducida se define como:

_El operador de evolución temporal infinitesimal es generado por el Hamitoniano.

transforma estados del tiempo al estado en el tiempo :

Donde
Donde es la funcion escalón de Heaviside

El operador de evolución temporal afecta a los estados:
Esto lleva a la ecuacion de Schrodinger

La ecuación de Schrodinger se reduce a un problema de autovalores del Hamiltoniano.

Si uno conoce los autovalores y autoestados del Hamiltoniano:

Cualquier estado puede ser escrito como combinacion lineal:

Por la ortogonalidad de los autoestados:
El operador evolución se puede expresar como:

El operador de evolución temporal afecta a los operadores:
Mientras que el estado no evoluciona. A partir de esto y la ecuación del operador evolución temporal, cumple:

Hamiltoniano de la forma:

Operador Evolución de :

Operador Evolución de :

Estado del sistema:
Operadores:
Los operadores evolucionan como en la representación de Heisenberg si el hamiltoniano fuese
Ecuacion de evolucion del estado:

Se trabaja con la versión adimensional de y con

La conmutación se convierte en: 𝟙

El hamiltoniano del oscilador armónico es:

Donde es el operador destrucción y es el operadoe creación.

Relaciones inversas:

Conmutador: 𝟙

Hamiltoniano del oscilador armonico cuantico:
𝟙El estado que satisface es el estado fundamental con función de onda: (Gausiana de ancho centrada en origen)

Los autoestados del hamiltoniano (estados estacionarios) cumplen: